Your awesome title

强连通分量

无向图的强连通分量相当的容易得到：图中不相连的部分自然构成了图的强连通分量（Figure 1）。如我们所见，深度优先搜索可以有效的解决这个问题：每次重新开始算法就是一个新的连通分量。 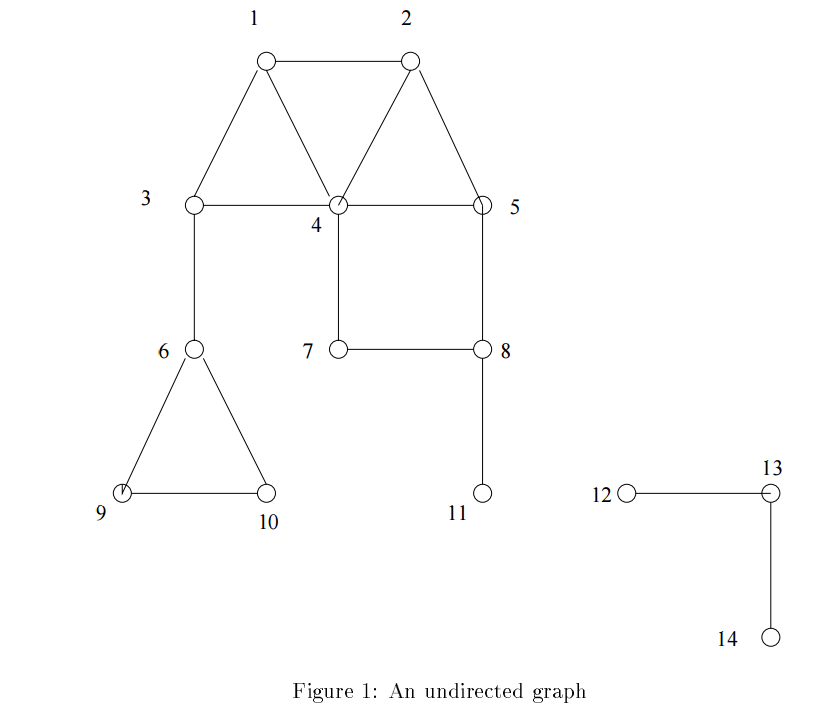Figure 1. An undirected graph | center | 300x0

有向图的强连通分量更加微妙。在有向图 $G=(V, E)$ 中两个节点u和v，如果存在从u到v的路径并且存在从v到u的路径，则称uv是连通的。在Figure 2中有四个强连通分量。

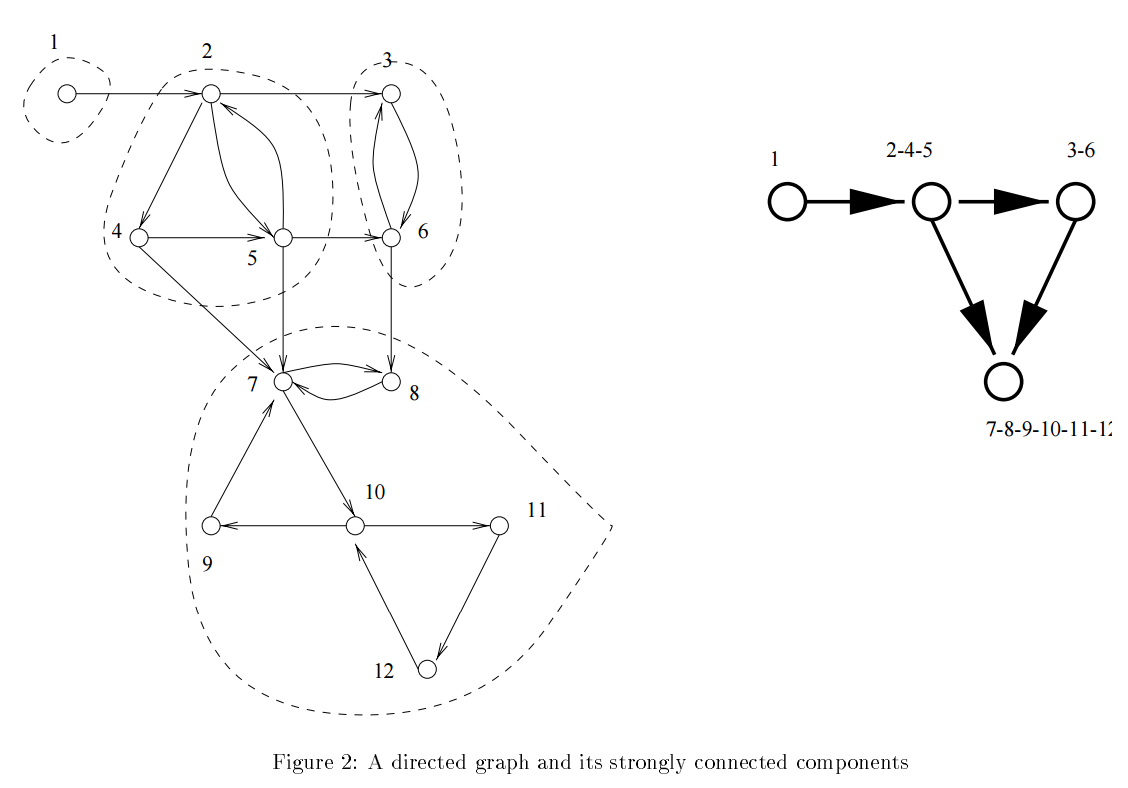
Figure 2. A directed graph and its strongly connected components

如果我们把每个强连通分量缩成一个单点，并且如果两个分量中的节点间存在边，则按该边的方向连接两个点，如此便构成了一个新的有向无环图（DAG）（Figure 2）。原因很简单：一个环包含多个强连通分量必然会将他们合并成一个。我们可以这么说：每个有向图是它的强连通分量的有向无环图

这一重要的结论允许我们可以分两层来求解有向图的强连通分量问题：

首先我们有个DAG——一个比较简单的结构。我们知道一个DAG至少有一个源点（入度为0的点）并且至少有个终点（出度为0的点），而且可以拓扑排序。
紧接着我们可以把DAG中的节点展开来干我们想干的事，每个展开节点都是一个强连通图。

如上的分解使得我们可以通过深搜（深度优先搜索）在线性时间内解决问题。讲算法之前我们先看一些结论：

Property 1 如果一个图的深搜开始于节点u，那么它将会遍历所有从u可达的点之后停止。因此，如果深搜开始于终点强连通分量中的一个节点（终点强连通分量即该强连通分量中没有边指向DAG中其他强连通分量），那么恰好它遍历完该强连通分量中的所有节点后就停止了。

如图Figure 2，如果深搜开始于节点11（图中唯一的终点强连通分量的一个节点），那么在遍历11，12，10，9，7，8（正好是终点强连通分量的六个节点）后停止。Property 1给出找到第一个强连通分量的方法：从终点强连通分量中一个节点开始遍历，停止后输出所有遍历过的节点，即构成了一个强连通分量！

当然，这留给我们两个问题

如何得到一个终点强连通分量中的节点
在输出第一个分量后如何继续输出第二，第三……

我们先来解决第一个问题。没有简单的直接解决办法，但是有方法可以得到源点强连通分量中的一个节点。

Property 2 深搜中最晚结束的节点（这里的结束是指先遍历完其他可达的节点后才算起始节点的结束，类似树的后序遍历，根是最晚结束的）属于源点强连通分量。

Property 2源于一个更基本的事实：

Property 3 C 和 C'是两个强连通分量并且存在一条由C中一个节点指向C'中一个节点的边，则深搜后C中这个先被访问的节点有比C'中任何一个节点都晚的结束时间。

Property 3的证明如下，存在有两种情况：C比C'先被访问，如此在深搜停止前已经访问完所有C和C'的所有节点，所以C起始访问节点具有最晚的结束时间。如果C'比C先访问，则在访问任何C的节点前深搜就停止了（C中的节点对于任何C'中节点不可达），所以结论仍然成了。

换种说法，Property 3可以如下描述：对图的强连通分量的拓扑排序既是将有向图的强连通分量按结束时间递减进行排序！这是广义的DAG拓扑排序算法。毕竟，DAG就是一个强连通分量为单个节点的有向图。

Property 2提供了一种间接的方法解决第一个问题：考虑图 $G = (V, E)$ ，图的反图就是图的所有边的方向反制，即 $G^R = (V, E)^R$ 。 $G^R$ 与原图有着相同的强连通分量。所以，我们对 $G^R$ 进行深搜，最晚完成的节点就是图 $G^R$ 源点强连通分量的一个节点——即原图 $G$ 的终点强连通分量的节点。所以第一个问题解决了！

再来看第二个问题：在终点强连通分量输出后如何继续呢？解决方法Property 3已经说明：在我们输出第一个强连通分量后把它从图中删除，在 $G^R$ 余下节点中深搜最晚完成的节点属于原图的余下部分终点强连通分量。因此，我们可以继续用 $G^R$ 深搜信息来得到第二个强连通分量，直到结束。完整的算法如下：

Step 1 在 $G^R$ 上进行深搜。

Step 2运用求解无向图强连通分量的算法，按step 1中得到的结束时间递减（由晚到早），处理原图的每个强连通分量。

以上算法是Kosaraju算法，wiki给出了Java的实现，下面是我在PTA数据结构与算法函数题第10题Strongly Connected Components的C实现

/*
typedef struct VNode *PtrToVNode;
struct VNode {
    Vertex Vert;
    PtrToVNode Next;
};
typedef struct GNode *Graph;
struct GNode {
    int NumOfVertices;
    int NumOfEdges;
    PtrToVNode *Array;
};
*/

Graph ReverseGraph(Graph G) {
    Graph g = (Graph)malloc(sizeof(struct GNode));
    (*g).NumOfVertices = (*G).NumOfVertices;
    (*g).NumOfEdges = (*G).NumOfEdges;
    (*g).Array = (PtrToVNode *)calloc(1, sizeof(PtrToVNode) * G->NumOfVertices);

    int count = G->NumOfVertices;
    for (int i = 0; i < count; i++) {
        PtrToVNode node = G->Array[i];
        while (node) {
            int ver = node->Vert;
            PtrToVNode now = (PtrToVNode)malloc(sizeof(struct VNode));
            now->Vert = i;
            now->Next = g->Array[ver];
            g->Array[ver] = now;
            node= node->Next;
        }
    }

    return g;
}

int stack[MaxVertices];
int visited[MaxVertices];
int k;

void DFS(Graph G, int node, void (*func)(int node)){
    visited[node]= 1;
    PtrToVNode vnode = G->Array[node];
    while (vnode) {
        if (!visited[vnode->Vert]) {
            DFS(G, vnode->Vert, func);
        }
        vnode = vnode->Next;
    }

    func(node);
}

void push(int node) {
    stack[k++] = node;
}

void SCC(Graph g, void (*visit)(Vertex V)) {
    memset(visited, 0, sizeof(visited));

    while(k > 0) {
        if (visited[stack[--k]]) {
            continue;
        }
        DFS(g, stack[k], visit);
        printf("\n");
    }
}



void StronglyConnectedComponents( Graph G, void (*visit)(Vertex V) ) {
    memset(visited, 0, sizeof(visited));
    Graph g = ReverseGraph(G);
    for(int i = 0; i < G->NumOfVertices; i++) {
        if (!visited[i]) {
            DFS(g, i, push);
        }
    }
    SCC(G, visit);
}

求解强连通分量

强连通分量

参考：